다익스트라(Dijkstra) 알고리즘
가중그래프에서 특정 하나의 노드에서 다른 모든 노드로의 최단 거리 정보를 알아내는 알고리즘이다.
음수 가중치를 갖는 간선을 포함한 그래프에서는 올바르게 동작하지 않는다. (음수 가중치가 있을 경우 최단 경로가 계속 갱신될 수 있기 때문에)
구현 특징
- 문제를 그래프로 표현하여 각 정점 연결 상황을 저장한다.
- 정점 간 최단 거리 정보(distance)를 1차원 리스트에 저장하며 리스트를 계속해서 갱신한다.
- 매 단계마다 아직 방문하지 않은 정점 중 최단 거리인 정점을 찾아 방문하여 최단거리를 확정하고, 이를 반복하는 방식이다.
- 방문하지 않은 정점 중에서 최단 거리가 최소인 정점을 찾는 과정에서 Heap, Priority Queue를 이용한다.
구현 방법
- 출발 노드(s) 설정
- 최단 거리 테이블(D) 초기화
- D[s] = 0
- D[v] = ∞ (v는 출발 노드 s가 아닌 모든 vertex)
- 방문하지 않은 노드 중 최단 거리가 최소인 노드를 선택한다.
- Heap / Priority Queue를 이용
- 가장 처음에는 출발 노드에서 인접한 노드들부터 확인
- 선택된 노드(v)는 방문 처리한다. 이 노드를 거쳐 다른 노드로 가는 거리를 계산하고, 최단 거리 테이블을 갱신한다. (v와 연결된 각 노드 u에 대해, dist[u]과 dist[v] + 'v에서 u으로 가는 비용'을 비교하여 후자가 더 작다면 테이블 갱신)
- 3-4번 과정을 모든 노드가 방문될 때까지 반복한다.
구현 코드
package shortestpath;
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.PriorityQueue;
import java.util.StringTokenizer;
public class Boj1753_최단경로 {
static int V,E,K;
static ArrayList<ArrayList<Node>> list;
static int dist[];
static class Node implements Comparable<Node> {
int number;
int weight;
public Node(int end, int weight) {
this.number = end;
this.weight = weight;
}
@Override
public int compareTo(Node n) {
return this.weight - n.weight;
}
}
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
V = Integer.parseInt(st.nextToken()); // 정점의 개수
E = Integer.parseInt(st.nextToken()); // 간선의 개수
K = Integer.parseInt(br.readLine()); // 시작 정점
dist = new int[V+1]; // 시작 정점으로부터 최단 경로
Arrays.fill(dist,Integer.MAX_VALUE);
list = new ArrayList<>();
for(int i=0; i<=V; i++) {
list.add(new ArrayList<>());
}
for(int i=0; i<E; i++) {
st = new StringTokenizer(br.readLine());
int from = Integer.parseInt(st.nextToken());
int to = Integer.parseInt(st.nextToken());
int weight = Integer.parseInt(st.nextToken());
list.get(from).add(new Node(to,weight));
}
dijkstra(K, V);
// 각 정점으로의 최단 경로의 경로값을 출력
for(int i=0; i<V; i++) {
// 경로가 존재하지 않는 경우 "INF" 출력
System.out.println(dist[i]==Integer.MAX_VALUE?"INF":dist[i]);
}
}
static void dijkstra(int start, int v) {
PriorityQueue<Node> q = new PriorityQueue<Node>();
dist[start] = 0;
q.add(new Node(start,0));
while(!q.isEmpty()) {
Node currentNode = q.poll();
int currentNum = currentNode.number;
// 이미 확정된 노드
if (dist[currentNum] < currentNode.weight) continue;
for(Node node: list.get(currentNum)) {
if(dist[node.number] > (dist[currentNum]+node.weight)) {
dist[node.number] = (dist[currentNum]+node.weight);
q.add(new Node(node.number,dist[node.number]));
}
}
}
}
}
백준 1753번 최단경로 문제에 대한 답으로, 간선 정보와 시작 정점이 주어졌을 때, 각 정점으로의 최단 경로의 경로값을 출력하는 코드이다.
예시 문제
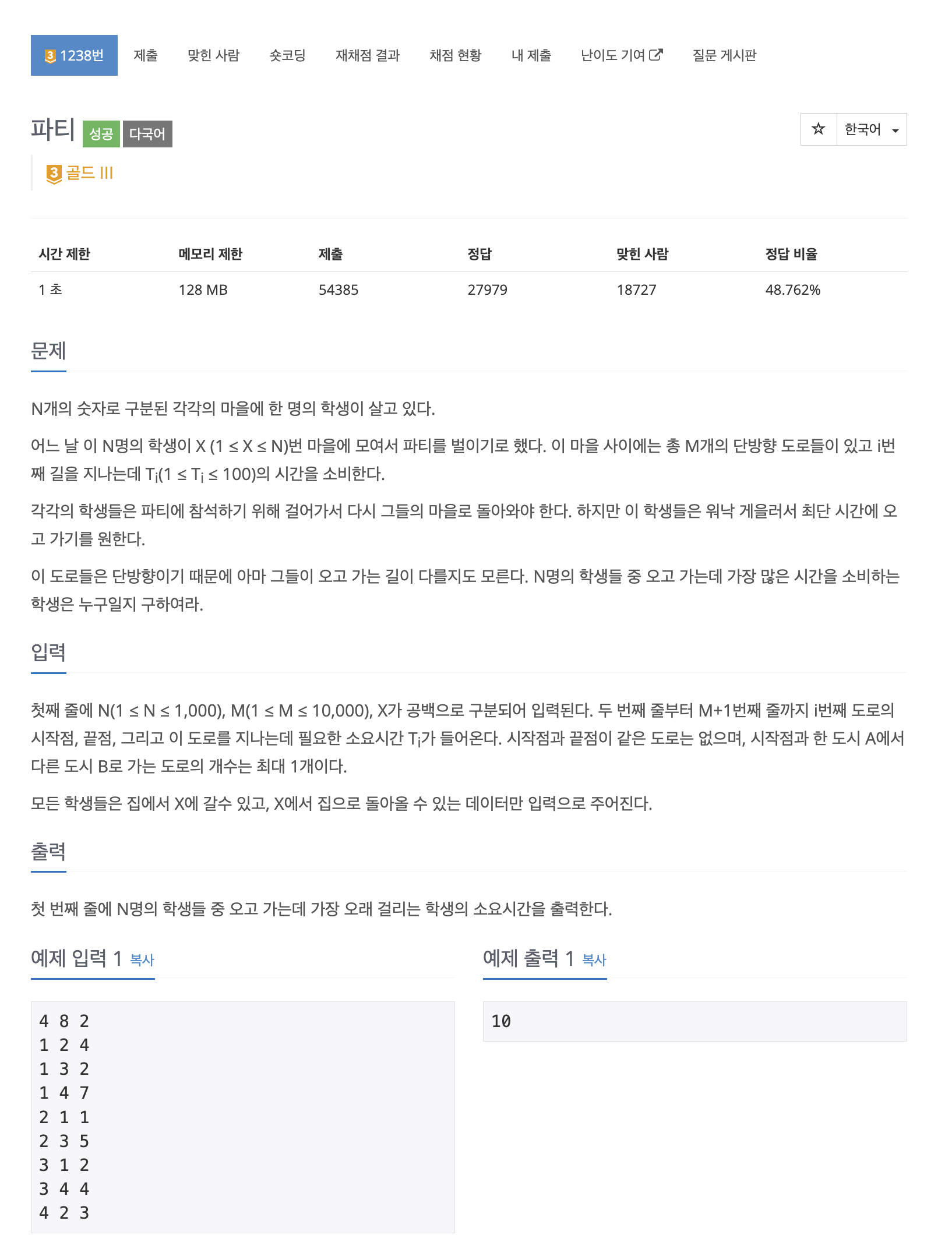
위 문제를 풀기 위해서는 다음 두 가지 정보를 알아내어야 한다.
1. 출발지 X에서 다른 모든 마을로 가는 최단 경로 (one to all)
2. 다른 모든 마을에서 X로 오는 최단 경로 (all to one)
1번째 정보는 원래의 다익스트라 알고리즘을 통해 알아낼 수 있다.
그렇다면 2번째 정보는 어떻게 알아내어야 할까?
🌟 다른 모든 노드에서 S로의 최단 거리 구하는 방법
가장 단순하게 생각하면 S가 아닌 모든 vertex를 출발지로 잡고 다익스트라 알고리즘을 돌려서 각 버전의 dist[X]를 알아내는 방법이 있다.
이 경우, 다익스트라 알고리즘을 vertex의 수만큼 돌려야 한다.
다른 방법이 있다.
출발점을 X로 잡는 대신, 기존 edge의 방향을 반대로 뒤집어 다익스트라 알고리즘을 돌리는 것이다.
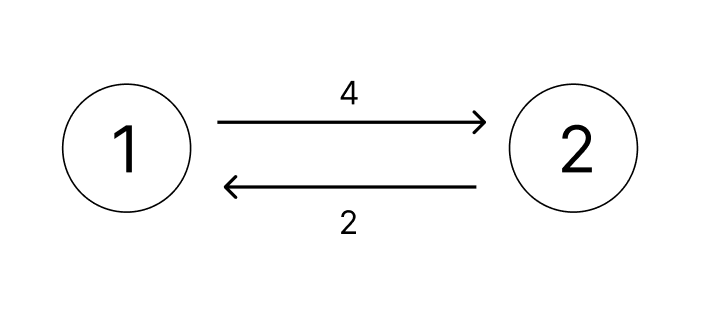
그래프 상황이 다음과 같고, 시작 정점이 1이라고 하자.
1에서 2로 가는 거리는 4이고, 이는 위에서 말한 첫번째 정보에 해당한다.
2에서 1로 오는 거리는? 간선의 방향을 반대로 뒤집으면 알 수 있다.
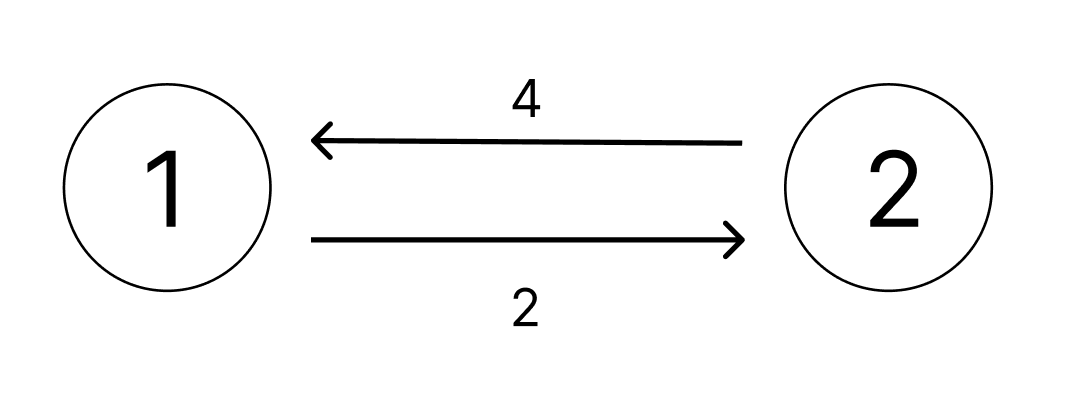
이렇게 간선을 반대로 뒤집고 출발점을 X로 잡은 후 다익스트라 알고리즘을 돌리면 다른 모든 vertex로부터 S로 오는 최단 거리를 알아낼 수 있다.
구현 코드
package shortestpath;
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.PriorityQueue;
import java.util.StringTokenizer;
public class Boj1238_파티 {
static int M, N, X;
static int[] dist;
static int[] reveresdDist;
static class Node implements Comparable<Node> {
int number;
int cost;
public Node(int number, int cost) {
this.number = number;
this.cost = cost;
}
@Override
public int compareTo(Node p) {
return this.cost - p.cost;
}
}
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
N = Integer.parseInt(st.nextToken());
M = Integer.parseInt(st.nextToken());
X = Integer.parseInt(st.nextToken());
ArrayList<ArrayList<Node>> connectList = new ArrayList<>();
ArrayList<ArrayList<Node>> reveresedConnectList = new ArrayList<>();
for(int i=0; i<=N; i++) {
connectList.add(new ArrayList<Node>());
reveresedConnectList.add(new ArrayList<Node>());
}
for(int i=0; i<M; i++) {
st = new StringTokenizer(br.readLine());
int from = Integer.parseInt(st.nextToken());
int to = Integer.parseInt(st.nextToken());
int cost = Integer.parseInt(st.nextToken());
connectList.get(from).add(new Node(to, cost));
reveresedConnectList.get(to).add(new Node(from, cost));
}
int distToGo[] = dijkstra(connectList);
int distToGoBack[] = dijkstra(reveresedConnectList);
int max = 0;
for(int i=1; i<=N; i++) {
if (distToGo[i] + distToGoBack[i] > max) {
max = distToGo[i] + distToGoBack[i];
}
}
System.out.println(max);
br.close();
}
static int[] dijkstra(ArrayList<ArrayList<Node>> list) {
int dist[] = new int[N+1];
Arrays.fill(dist, Integer.MAX_VALUE);
dist[X] = 0;
PriorityQueue<Node> pq = new PriorityQueue<Node>();
pq.add(new Node(X, 0));
while(!pq.isEmpty()) {
Node currentNode = pq.poll();
int currentNumber = currentNode.number;
for(Node node: list.get(currentNumber)) {
if(dist[node.number] > dist[currentNumber] + node.cost) {
dist[node.number] = dist[currentNumber] + node.cost;
pq.add(new Node(node.number, dist[node.number]));
}
}
}
return dist;
}
}
'알고리즘 > study' 카테고리의 다른 글
| 플로이드-워셜(Floyd–Warshall) 알고리즘 (0) | 2024.11.06 |
|---|---|
| 벨만-포드(Bellman-Ford) 알고리즘 (0) | 2024.11.05 |
| 투포인터(Two Pointer) 알고리즘 (1) | 2024.03.04 |
| 그래프 탐색 DFS, BFS (1) | 2024.01.27 |
| 누적합(Prefix Sum) (1) | 2024.01.23 |